前回に引き続き、現代金融理論(Modern Monetary Theory: MMT)について、Palley(2015)を元に解説する。
前回:現代金融理論MMT解説(1):目新しくないのに実現は難しい
今回取り上げるのは物価と産出量の関係を説明するAD-AS分析から捉えたMMTの内容である。まず、ケインズ経済学の枠組みにおいて、AD(総需要)曲線とAS(総供給)曲線の関係は以下の通りになる。
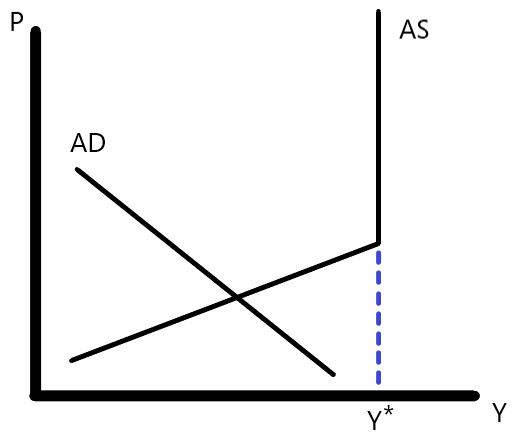
出典:筆者作成
IS-LM曲線などの外生変数を無視すれば、総需要曲線ADは以下のように表せる。
$$Y=AD(G,\frac{M}{P})\tag{1}$$
ここでGは政府支出、Mは名目貨幣供給量(マネーサプライ)、Pは物価水準である。財政支出や貨幣供給量を増加させるとAD曲線は右にシフトし、完全雇用に近づいていくが、少しずつインフレが起こる。完全雇用\(Y^*\)が達成されると、貨幣供給量を増やしてもこれ以上生産が増えないので、総供給曲線ASは垂直になる。
では、MMTだとどうなるだろう。まず、前回書いたMMT論者の中心的な主張を再掲する。
自国通貨で国債を発行している政府であれば、中央銀行が債務の利率を決定できるので、中央銀行に紙幣を発行させればデフォルトすることはなく、完全雇用を実現して財政赤字が深刻な影響をもたらすようになるまで増税する必要はない
太字で示した「完全雇用を実現して財政赤字が深刻な影響をもたらすようになるまで」というのは平たくいえばインフレのことである。逆に言えば「完全雇用を実現するまではインフレにはならない」ということである。
これをAD-AS分析の枠組みで見たのが下図である。完全雇用\(Y^*\)でAS曲線が垂直なのは変わらないが、完全雇用に達しない場合は物価Pが一定となっており、AS曲線はL字型をしていることが分かる。
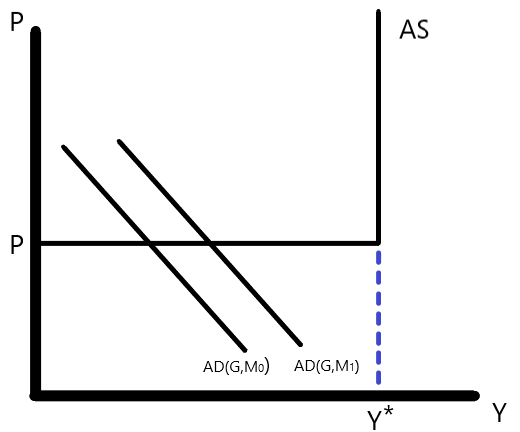
出典:Palley(2015: 15)より筆者作成
このように都合よくインフレをもたらさずに完全雇用を達成できるという仮定がどこからきたのかPalley(2015) も疑問を呈しているが、仮にこの仮定が妥当だとしても現実的には問題がある。というのも、これはあくまでも1部門経済だけの話である。経済には複数の部門が存在し、それらが同時に完全雇用が満たされると想定するのは不自然であり、複数部門の場合を考えなければならない。
そこで、仮に単純に2部門しか存在しない経済を考え、片方のみ完全雇用が達成された状態を考えたのが下図だ。部門1は完全雇用が達成されていないが、部門2は完全雇用が達成されていると仮定しよう。

出典:Palley(2015:16)を修正
この時、貨幣供給量の増加を行えば、両部門のAD曲線は右にシフトする。部門1なら\(AD_{1,0}\)から\(AD_{1,1}\)に、部門2なら\(AD_{2,0}\)から\(AD_{2,1}\)に シフトする。この時、部門1ではインフレは発生しない(価格は\(P_{1,0}\)のまま)が、部門2ではインフレが発生する。(\(P_{2,0}\) から\(P_{2,1}\)に物価上昇)
この場合、全体で見れば産出量Yは完全雇用には届いておらず、物価は少し上昇しているはずで、L字型にならない。つまり、複数部門になれば、部門ごとの雇用の状態によってインフレが発生するタイミングの予想が難しく、部門毎の状況に大きな差があれば完全雇用から程遠い場合でもインフレが発生する場合もあり、そうなると通常のAS曲線と変わらなくなる。要するにMMTが適用可能な経済というのは非常に限定されている(全ての部門が等しく完全雇用に達していない状態)というわけだ。
この上でPalley(2015)は 、MMTは物価と産出量のトレードオフを無視しており、動学的に考えればインフレ率と失業率のトレードオフであるフィリップス曲線を無視していると指摘している。フィリップス曲線を無視してインフレを起こさずに完全雇用を実現できるというのは無理な仮定であり、批判の対象となっている。
参考文献
Palley, Thomas I. “Money, fiscal policy, and interest rates: A critique of Modern Monetary Theory.” Review of Political Economy 27.1 (2015): 1-23.