民主党の米国大統領選候補者の一人で、AOC現象を代表するアレクサンドリア・ オカシオ・コルテス議員が信奉する非主流派経済学である現代金融理論MMT(Modern Monetary Theory)が日本でも話題になってきた。パウエルFRB議長が一蹴するなど現状では相手にされていないが、グリーンニューディールの財源確保の為に一部で盛り上がっているので、2回にわたり解説していく。
理論的に説明すると言っても、「これがMMTの標準的な理論」というものが示されているわけではなく、論者によって曖昧である部分が多い。そこで本稿では、マクロ経済学者トーマス・パリーによる理論的な整理と反論であるPalley(2015)を元に議論する。Palley(2015) では数多くの問題点が整理されているが、ここでは筆者なりの解釈で、
- 目新しい理論ではないのに政治的に難しい(本稿)
- 無理な仮定と非現実性(次項)
の2点に分けて解説する。
Palley(2015)はMMTを「よく知られたケインズ経済学を過剰に単純化(over-simplified)したもの」と評しており、本論でもSimple Keynesianの枠組みで整理されている。論文ではケインズ経済学の基礎の理解を前提としているが、本稿では基礎部分を補足しながら、より多くの人が理解できるように書いていく。
中央銀行の独立性の問題
MMTの中心的な主張は、自国通貨で国債を発行している政府であれば、中央銀行が債務の利率を決定できるので、中央銀行に紙幣を発行させればデフォルトすることはなく、完全雇用を実現して財政赤字が深刻な影響をもたらすようになるまで増税する必要はない、というものである。
要するに財政ファイナンスを行うことであり、日本が同じ状況だという見方もできる。しかし、日本は曲がりなりにも財政再建の重要性を認識しており、はじめから「紙幣を刷って返します」と開き直っているわけではない。なので、MMTを真正面からやろうとすれば長期的には国債を買ってくれる人がいなくなる、というのが反対者に共通する意見である。
増税に頼らずに支出を賄うということになれば、
- T:税収
- G:政府支出
- θ:国債発行額
- β:国債返済額
とすれば、以下が成立する。
$$T+\theta =G-\beta\tag{1-1}$$
変形して以下のようになる。
$$G-T =\theta+\beta\tag{1-2}$$
実際にこれを実行するとどうなるか、そして可能なのかが問題である。多くの国で(少なくとも表面的には)政府と中央銀行は独立しているのであり、この均衡条件を維持するように両者が堂々と協調して行うことは政治的に難しいというのが第一の問題点だ。
政策割当論
MMTをマクロ経済学的に簡潔に言えば「完全雇用を達成するまで財政支出もしくは減税」である。これを標準的なAD-ASモデルで考えると次のようになる。
$$y={ y }^{ * }=AD\left( G,T \right)\tag{2}$$
$$AD_G>0, AD_T<0$$
それぞれの記号の意味は以下の通りである。
- \(y \) :現在の産出量
- \(y^*\):完全雇用時の産出量
- \(AD\):総需要の関数
但し、総需要の関数ADにおいて、MMTでは政府支出Gに制約が無く、「財政赤字が深刻な影響をもたらすようになるまで増税する必要はない」という定義より、完全雇用が達成するか大きな問題が生じた場合は増税(Tを増加)させる必要がある。
これは図で示すと、以下の縦軸を総需要AD、横軸を産出量yとした時、現在の産出量\(y_1\)から完全雇用産出量\(y^*\)にまでシフトする動きを示している。いわゆる有効需要の原理を表したものである。
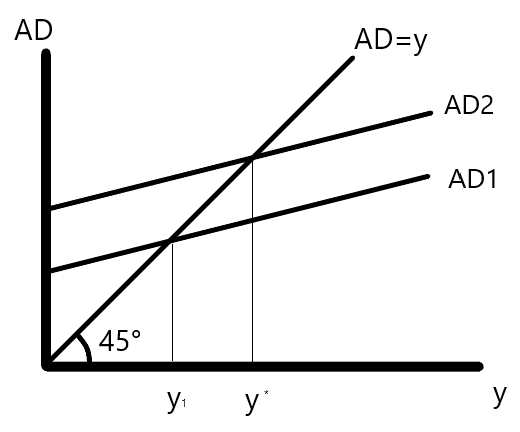
出典:筆者作成
上記の「財政赤字による深刻な影響」というのは、経済成長していない場合に、一貫して財政赤字を増やし続ける(紙幣を発行し続ける)ことでインフレを引き起こすことである。よって、通貨価値を維持するために以下の制約条件を満たさなければならない。
$$D = G – T\left(y^*, t\right) = 0\tag{3}$$ $$T_{y^*}>0, T_t>0$$ここでDは財政赤字であり、\(t\)期に完全雇用\(y^*\)が達成された場合、増税によって税収Tを増やし、財政赤字をゼロにしなければならないことを意味する。
この時、式(2)と(3)で重要なのは、この枠組みで政府は「\(y=y^*\)」と「\(D=0\)」という2つの目標を抱えるということである。
ティンバーゲン=マンデルの政策割当論によれば、「n個の政策目標を同時に達成するには別個の政策がn個必要」(ティンバーゲンの定理)であり、「各目標にどの政策を割り当てるかについては、最も安価に実現できる手段を用いるべき」(マンデルの定理)である。
この時、マクロ経済学の乗数効果から考えれば「財政支出Gで産出\(y=y^*\) を実現」し「増税tで\(D=0\) を実現」するということになる。
輸出・輸入を考えなければ、所得Yは(4-1)と表現できる。(Cは消費、Iは投資)
$$Y=C+I+G\tag{4-1}$$
消費Cは(4-2)のように表現できる。aは限界消費性向(所得Yが1単位増えた時に消費に回す割合)である。(厳密にはケインズ型の消費関数は\(C=aY+C_0)と基礎消費が入るが、ここでは数式を簡単にするためにクズネッツ型を用いる。)
$$C=aY\tag{4-2}$$
$$0<a<1, 0<b$$
式(4-1)と(4-2)より、
$$Y=aY+I+G$$
$$(1-a)Y=I+G$$
$$Y=\frac{1}{1-a}I+\frac{1}{1-a}G\tag{4-3-1}$$
では財政政策により、財政支出GがG’に増加し、YがY’に変化したとすれば、(4-3-1)より、
$$Y’=\frac{1}{1-a}I+\frac{1}{1-a}G’\tag{4-3-2}$$
(4-3-2)から(4-3-1)を引けば、
$$Y’-Y=\frac{1}{1-a}\left(G’-G\right)\tag{4-4}$$
となる。\(0<a<1\)より\(\frac{1}{1-a}>1\)なので、財政支出Gの増加より所得Yの増加の方が多い。これが乗数効果である。(\(\frac{1}{1-a}>1\) が政府支出乗数)
次に税金Tを導入すれば、(4-2)の消費関数は以下のようになる。
$$C=a(Y-T)\tag{5-1}$$
財政政策の場合と同様に変形すれば、(4-3-1)に対応するのは以下である。
$$Y=-\frac{a}{1-a}T+\frac{1}{1-a}I+\frac{1}{1-a}G\tag{5-2}$$
同様に税金TをT’に減税した時、所得YがY’に変化したとすれば、
$$Y’-Y=-\frac{a}{1-a}\left(T’-T\right)\tag{5-3}$$
であり、Tを1単位減らした時、Yは減税乗数\(\frac{a}{1-a}\)だけ増加する。
1-a}\)だけ増加する。
政府支出乗数と減税乗数を比較した時、政府支出乗数の方が大きい。例えば\(a=0.6\)なら、\(\frac{1}{1-a}=2.5\)と\(\frac{a}{1-a}=1.5\)であり、先に述べた通り、財政支出Gの増加によって完全雇用を達成すべきであることが分かり、残った税金Tの増加で財政均衡化を達成するという政策割当が妥当になる。
MMTで言っていることは基本的にこれと同じことであり、特に目新しいものではないことが分かる。目新しくないが、財政均衡化目標を大幅に緩める(大きな問題が生じるまで財政赤字は気にしない)という意味で不安定なものになっており、政治的に難しいものになっている。
では、財政規律を気にしなくて大丈夫なのかについてMMTがどう答えているかについては次回に説明しよう。
参考文献
Palley, Thomas I. “Money, fiscal policy, and interest rates: A critique of Modern Monetary Theory.” Review of Political Economy 27.1 (2015): 1-23.