AI人材が足りないと言いつつ、2015年度から高校数学から「行列」が消え、2022年度から「ベクトル」が数Cに移動するなど、線形代数の基礎を学ばずに大学に進学する高校生が今後ますます増えていく。(復活も検討されているようだ。また、代わりにデータ分析などは追加されている。)
統計も重要であるが、線形代数はAIに限らずいわゆる「今後伸びそうな分野」において密接に関連するケースが多い。
人工知能(AI)は言わずもがな、ゲームでCGを扱いたい、ARやVRをやってみたいとなれば、必ず線形代数の知識が求められる。IoTで位置情報と紐付いたセンサーデータを利用するにしても必要だし、ドローンを遠隔制御するのにだって必須である。要するに、こうした流行り物の技術のベースに線形代数は必要である。
線形代数の教科書と言えば『線形代数入門(基礎数学1)』(東京大学出版会)である。教科書としては非常に分かりやすいが、いわゆる「数学が苦手な人」にとっては自力で読むのはハードルが高いかもしれない。「入門」というのは研究者目線での話である。

数学的なトレーニングを受けていない人にオススメできるのが志賀浩二氏の「数学30講シリーズ」(朝倉書店)である。『線形代数30講』は鶴亀算から始まるので、高校数学を全て忘れた、行列もベクトルも何もやっていないという人でも読める。基本的に2次元・3次元までに話を限定しているのでイメージもしやすく、数学が苦手な人でも挫折しにくいと思われる。

もっとも、これに関しては固有値問題の触りまでしかされないので、これだけでも一般的な知識としては十分だが、専門的に扱うなら更に知識が必要である。これを読んだ上で上記の『線形代数入門』に入るのも良いかと思われるが、もうワンクッションが必要な場合もあるだろう。
その時は同じく「数学30講シリーズ」の『固有値問題30講』が良い。固有値や基底の概念、ジョルダンの標準形など線形代数の基礎が十分に盛り込まれている。

なお、30講シリーズはファンが多い一方でアンチも多い。数学的な厳密性を捨象している部分があり、証明が一部簡略化されているケースも多いからである。しかし、いきなり専門書から入って挫折するくらいなら、こうした一般書から着実に進んでいく方が結果的に良いと筆者は考えている。
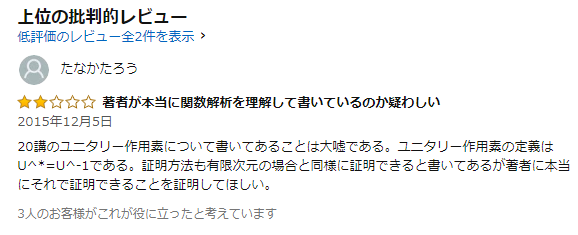
なお、固有値問題の方には以下のようなレビューがある。
第20講でユニタリー作用素の定義として、
ユニタリー作用素: U*U=I(恒等作用素)をみたす有界作用素Uを、ユニタリー作用素という。
志賀(1991: 162)
とあり、
$$U^*U=I$$ではなく、
$$U^*=U^{-1}$$だと言いたいらしい。
しかし、ユニタリー作用素は正則なので、テキストの式の両辺に\(U\)の逆行列である\(U^{-1}\)を右からかければ、ちゃんとレビューで指摘されている定義の式になる。別のテキストの定義と違ったから条件反射的に批判したのと思われる。